Introduzione
Salve lettori, questa pagina è stata creata per riassumere o ampliare gli appunti che prendiamo a lezione, questi appunti possono servire per capire meglio l’argomento e non possono essere capiti completamente se non si seguono le lezioni. Se trovate errori o parti poco chiare vi prego di segnalarlo così provederemo a corregere. Buona lettura -NP
Capitolo Uno: Proprietà dell’algebra
Le 10 proprietà dell’algebra sono fondamentali per riiuscire a capire come siamo arrivati alle tecniche di semplificazioni dei giorni d’oggi.
Elemento neutro
- a + 1 = 1
- a + 0 = a
- a * 0 = 0
- a * 1 = a
Idempotenza
- a + a = a
- a * a = a
Inverso o Complemento
- a + \neg a = 1
- a * \neg a = 0
Commutativa
- a + b = b + a
- a * b = b * a
Associativa
- a + (b + c) = (a + b) + c
- a * (b * c) = (a * b) * c
Distributiva
- a * (b + c) = a * b + a * c
- a + (b * c) = (a + b) * (a + c)
Assorbimento
- a + (a * b) = a
- a * (b + a) = a
- a + \neg a * b = a + b
- a * (\neg a +b) = a * b
Leggi di De Morgan
- \neg (a + b) = \neg a * \neg b
- \neg (a * b) = \neg a + \neg b
Consenso
- a * b + \neg a * c + b * c = a * b + \neg a * c
- (a + b) * (\neg a + c) * (b + c) = (a + b) * (\neg a + c)
Principio di Dualità
Ogni formula logica può essere trasformata in un’altra se:
- ogni + diventa * e viceversa.
- ogni 0 diventa 1 e viceversa.
Capitolo Due: Teorema di Shannon e mappe di Karnaugh
2.1 Teorema di espansione di Shannon
Teorema di Espansione di Shannon: Data f(a,b) posso scriverla come a f(1,b) + \neg a f(0,b).
Dimostrazione
a = 1 \implies f(1,b) = 1f(1,b) + 0f(0,b) visto che a = 1 \implies \nexists 0 \to = f(1,b) si potrebbe espandere anche per b quindi a(bf(1,1) + \neg b f(1,0)) + \neg a (bf(0,1) + \neg b f(0,0)).
2.2 Mappa di Karnaugh
Logica che sta dietro Karnaugh: l’idea di Karnaugh è una rivoluzione a livello logico, ovvero lui ha pensato di poter rendere visibili gli 0 e 1 delle formule logiche mettendole su quadrati di N dimensioni.
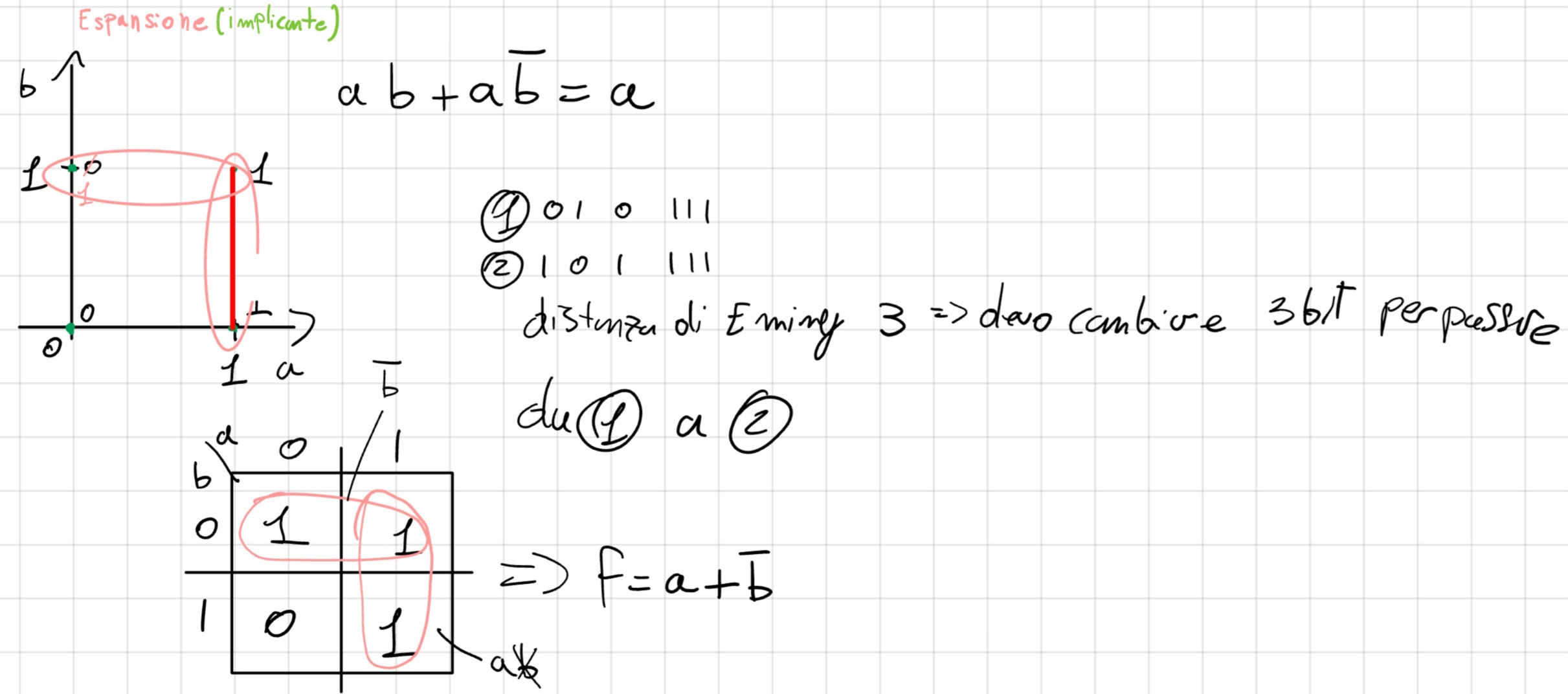
Distanza di Hamming: distanza minima per poter portare una sequenza di bit da una forma a un’altra.
Esempio per portare 011 a 100 la distanza di Hamming è 3 visto che devo cambiare tutti e 3 i bit, la distanza di Hamming di 10 a 11 è 1 visto che devo cambiare solo 1 bit.
Questo ci serve per capire le mappe di Karnaugh dalla 3 alla n-esima dimensione visto che i bit devono avere distanza di Hamming 1 tra loro per poter conservare le proprietà dell’algebra e perchè essendo quandratia 3, 4, n-esima dimensione tra di loro devono essere adiacenti gli angoli.
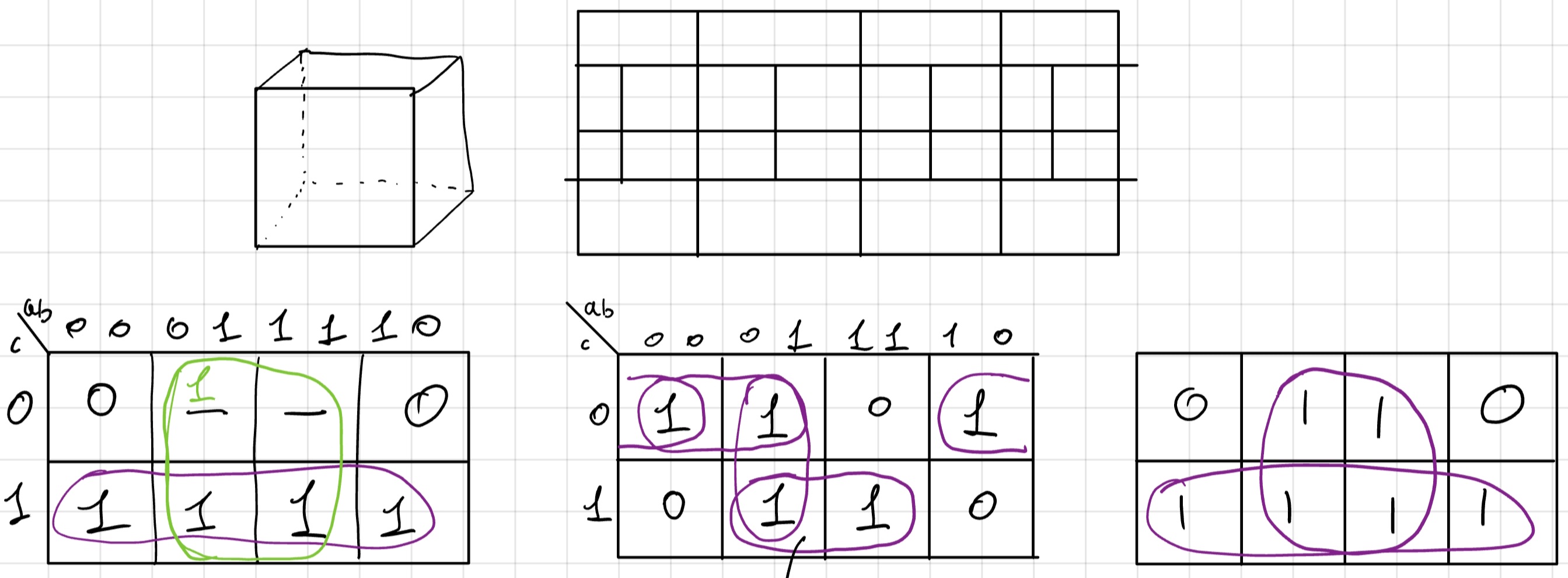
Possiamo notare qui che si passa da un quadrato a 3 dimensioni a una mappa dove le caselle 10 e 00 sono adiacenti.
Ora per la quarta dobbiamo immaginare un quadrato a 4 dimensioni, cosa molto difficile ma fattibile, diventerà più difficile immaginarlo a n dimensioni quindi conviene ragionare tramite matrici.
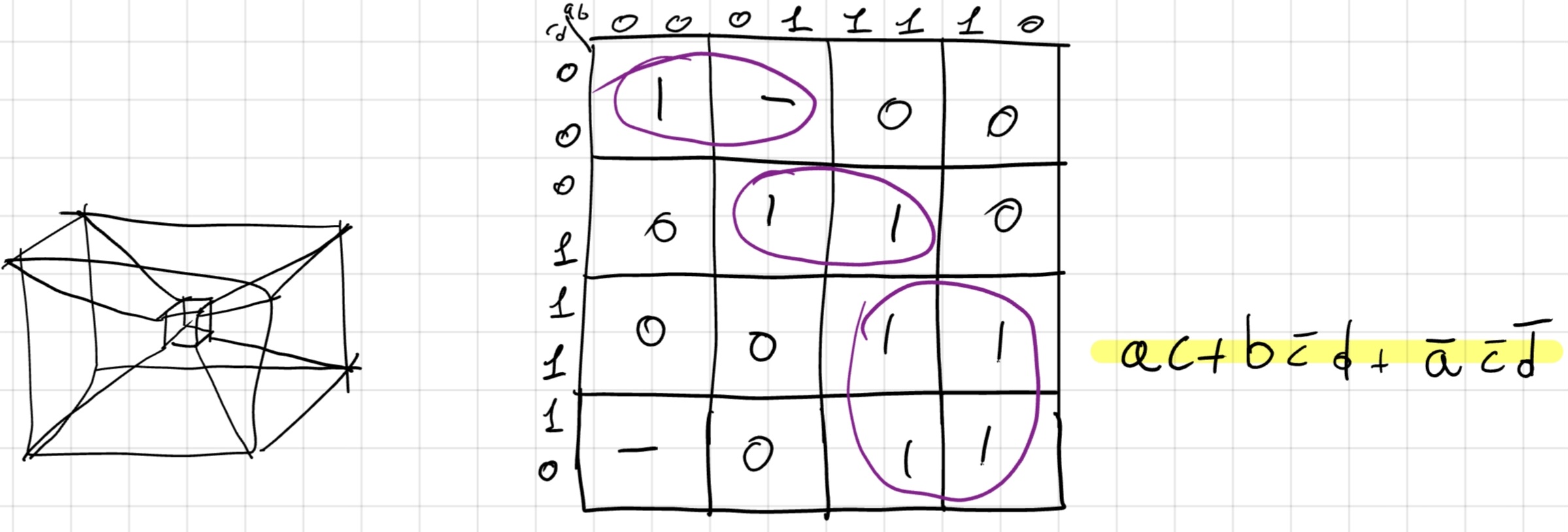
Don’t care: i simboli “-” stanno ad indicare un Don’t care, ovvero un simbolo che non ci interessa visto che l’ambiente non potrà mai generarlo, dunque noi lo consideriamo come meglio ci torna.
I raggruppamenti tra 1 sono da fare a potenze di 2, quindi 1, 2, 4, 8, 16, etc.
Raggruppamenti primi sono tutti i raggruppamenti massimi che sono possibili fare in una mappa di Karnaugh tra 1, considerando che sono leciti solo raggruppamenti verticali e orizzontali.
Raggruppamenti essenziali: sono tutti quei raggruppamenti che sono essenziali per raggruppare gli 1, ovvero quei raggruppamenti che se non fatti lascerebbero solo un 1.